
Challenge #7 – The Josephus Problem
In this mythical-historical mathematical problem, where you end up standing can be the difference between life and death. We’ll let Numberphile explain the problem and solution in the following video.
Challenge
The challenge is to write a twig macro that accepts at least one parameter n (an integer representing the total number of people in the circle) and outputs the position in which one must initially stand in the circle in order to be the last person standing and therefore the only survivor.
{% set n = 41 %}
{{ josephus(n) }} // Outputs 19
An online search will yield various approaches to solving this problem, but the challenge here is to come up with your own twig-specific solution using the information provided in the video.
Rules
The macro must output an integer as the solution, given the parameter as described above. It should not rely on any plugins and the code will be evaluated based on the following criteria in order of priority:
- Originality
- Readability
- Brevity
The algorithm you use should be based around one of the solutions presented in the video. The code should be readable, concise and non-repetative.
Tips
The problem can be solved in twig using either an iterative or a recursive approach. We covered recursion in a previous challenge (#4) and this may be a good opportunity to put your understanding of it to the test.
Solution
The mathematical formula to the problem is provided in the video and can be summarised as follows.
If n = p + L, where n is the total number of people and p (referred to as 2a in the video) is the greatest power of 2 that is less than n, then the winning position is 2L + 1.
In order to write an algorithm that uses this formula, we simply need to calculate p, the greatest power of 2 that is less than n, and then we can calculate L as L = n - p.
We begin with an iterative approach in which we begin with p = 1 and increase the power of 2 until we reach a number that is greater than n.
{% set p = 1 %}
{% for i in 0..n %}
{% if p <= n %}
{% set p = p * 2 %}
{% endif %}
{% endfor %}
After the loop has completed, we are left with a value for p that is one power of 2 greater than n. So we simply divide p by 2 to get the correct value.
{% set p = p / 2 %}
Now all that is left is to calculate L and plug it into the formula above to output the solution.
{% set L = n - p %}
{{ (2 * L) + 1 }}
Putting this all together in a macro gives us the following iterative solution.
{% macro josephus(n) %}
{% set p = 1 %}
{% for i in 0..n %}
{% if p <= n %}
{% set p = p * 2 %}
{% endif %}
{% endfor %}
{% set p = p / 2 %}
{% set L = n - p %}
{{ (2 * L) + 1 }}
{% endmacro %}
{% from _self import josephus %}
{{ josephus(n) }}
We clearly do not need to iterate over the entire range of 0..n to find p, but since we do not have the equivalent of a while loop in twig, we take the performance hit (the number of times would actually be Log2n).
Similar solutions: Spenser Hannon.
A recursive approach is also possible, since in each iteration above we are solving a subset of the problem. In the recursive approach, we keep track of the value of p using a second parameter.
{% macro josephus(n, p) %}
{% if p <= n %}
{% from _self import josephus %}
{{ josephus(n, p * 2) }}
{% else %}
{% set p = p / 2 %}
{% set L = n - p %}
{{ (2 * L) + 1 }}
{% endif %}
{% endmacro %}
{% from _self import josephus %}
{{ josephus(n, 1) }}
The result is the same, but note how we recursively call the macro only as long as p <= n. As soon as that condition does not hold true, we output the calculated result.
So we have gone from an iterative solution with a time complexity of O(n) to a recursive one with a time complexity of O(Log2n).
The algorithms above are based on the mathematical solution presented in the video and are performant ways of calculating the result. We could also take a different approach and try to solve the problem more “computationally”. For example, rather than working with the values n and p, we could begin with an array of the range 1..n and remove a value from it in each recursive call until we are left with an array with only a single value, the result.
{% macro josephus(people, next) %}
{% if people|length > 1 %}
{% set next = next % people|length %}
{% set people = people|slice(0, next)|merge(people|slice(next + 1)) %}
{% from _self import josephus %}
{{ josephus(people, next + 1) }}
{% else %}
{{ people[0] }}
{% endif %}
{% endmacro %}
{% from _self import josephus %}
{{ josephus(1..n, 1) }}
This macro takes as parameters an array people and an integer next which represents the 0‑index position of the next person to be removed. If the value of n is greater than the number of remaining people then we use its modulo value. We then manipulate the people array using the slice and merge filters to remove the value at position next. This is rather poor implementation in terms of performance as rather than working with an integer as we did in the previous solutions, we are working with arrays.
Below is a comparison of the performance profiling of the 3 approaches described above using the Twig Profiler plugin and a value of n = 4100 (to help exaggerate the differences).
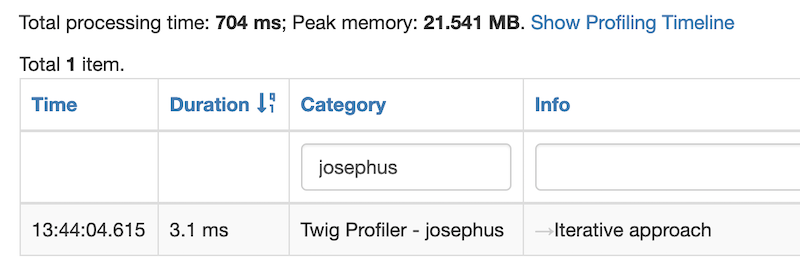
Iterative Approach
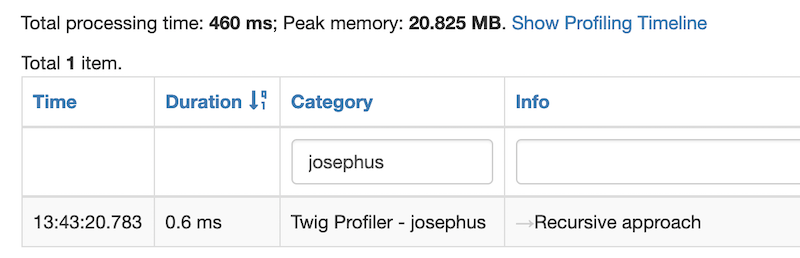
Recursive Approach
Using Arrays
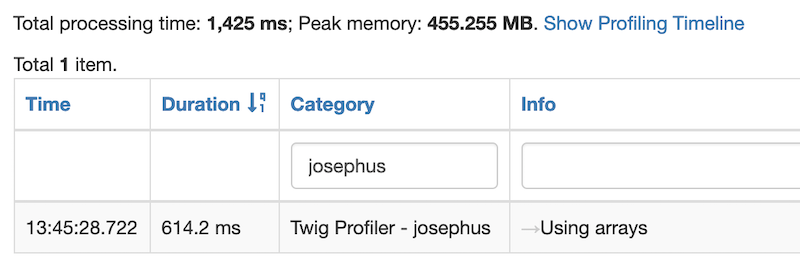
It is obvious to see that the recursive approach is by far the most performant with a processing time of only 0.6ms and a peak memory of 20MB. The iterative approach comes in second place with a processing time of 3.1 ms and a peak memory of 21MB. The performance hit is because of the unnecessary iterations that it performs. In last place is the approach using arrays with a whopping processing time of 614.2ms and a massive peak memory of 455MB. This is due to the fact that we are manipulating arrays with thousands of values in them. It would have been made even worse had we used an iterative approach in the solution.
The performance profiling presented above will hopefully encourage you to take caution when writing algorithms that manipulate arrays within loops or recursive functions. This applies in any programming language and can even affect what might be considered as common manipulations such as using an array_merge within a loop in PHP.
$values = [];
foreach ($arrays as $array) {
$values = array_merge($values, $array);
}
A more performant way, as explained here, is to modify the code and use the array_merge operation only once at the end.
$valueSets = [[]];
foreach ($arrays as $array) {
$valueSets[] = $array;
}
$values = array_merge(...$valueSets);
Here we use argument unpacking to unpack the array $valueSets into an argument list using the “splat” operator … (gotta love the naming), thereby reducing the number of merges to one. The results of these benchmarks show that there is significant performance to be gained.
Submitted Solutions
- Spenser Hannon
Solution submitted by Spenser Hannon on 7 February 2019.
{% macro josephus(number) %}
{%- set pow = 1 -%}
{%- for i in 0..number if pow < number -%}
{%- set pow = pow * 2 -%}
{%- endfor -%}
{%- if pow > number -%}
{%- set pow = pow / 2 -%}
{%- endif -%}
{{ (number - pow) * 2 + 1 }}
{% endmacro %}