Challenge #5 – Napkin Navigation

You have been con­tac­ted by an anonym­ous stranger to help meet a very tight dead­line. The stranger has only a few hours to vis­it spe­cif­ic houses and deliv­er a spe­cial pack­age to each of them. You have been giv­en a com­plex for­mula in the form of a line of twig code that when executed reveals the next house to vis­it, how­ever the code is far too cumbersome. 

There’s no time to lose, you must reverse engin­eer a com­plex for­mula to some­thing that any­one can cal­cu­late, even while steer­ing a herd of reindeer through the dark. All you have to work with is a nap­kin and your cunning.

{{ (max(range(n, 1, 2)|batch(4)[1]) + n) / 2 % 4 }}

The twig code takes a pos­it­ive integer n and out­puts a num­ber between 0 and 3, each sig­nal­ing the dir­ec­tion in which to move along the map to reach the next house. You have been giv­en a nap­kin with the map along with a legend of the directions. 

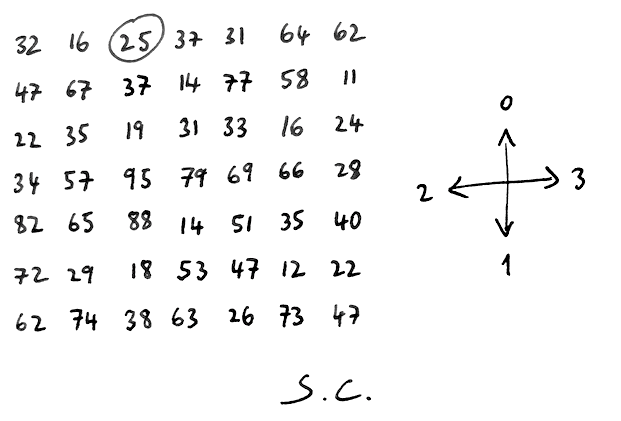
Your chal­lenge is to sim­pli­fy the for­mula so that for each house num­ber n, the dir­ec­tion to turn can be cal­cu­lated as quickly as pos­sible. Once you’ve done that, help the stranger by cal­cu­lat­ing the route to take through the map of houses.

Chal­lenge

The chal­lenge is to refact­or the for­mula above to its simplest form. Then use it to cal­cu­late the path through the map of house num­bers, start­ing at the circled house num­ber and cal­cu­lat­ing the dir­ec­tion to move for each house num­ber n, end­ing when you run out of numbers.

Rules

The for­mula should be refact­ored so that it is easy to cal­cu­late in your head. The for­mula as well as the route of house num­bers should be submitted.

Tips

This is a twig-only chal­lenge that you can lit­er­ally solve on a nap­kin, so you don’t even need to leave the din­ner table!

Hat tip to Lind­sey DiLoreto and Andrew Welch for their sug­ges­tions and input.

Solution

Let’s begin by break­ing down the twig code into its vari­ous com­pon­ents. This will allow us to parse it in the cor­rect order.

{{ (max(range(n, 1, 2)|batch(4)[1]) + n) / 2 % 4 }}

The first part of the for­mula is a max func­tion which itself con­tains a range func­tion. Eval­u­at­ing range(n, 1, 2) res­ults in an array of num­bers start­ing at n and end­ing at 1 with a step of 2 (the value to incre­ment or decre­ment, as is the case).

[ n, n-2, n-4, n-6, n-8, n-10, n-12, n-14, ... ]

To this we need to apply the batch fil­ter with a batch size of 4, which will res­ult in an array of arrays (a multi-dimen­sion­al array), each con­tain­ing 4 elements.

[ [ n, n-2, n-4, n-6], [ n-8 , n-10, n-12, n-14 ], ... ]

We then fetch the ele­ment at pos­i­tion 1, which is the second ele­ment since array indexes always start at 0.

[ n-8 , n-10, n-12, n-14 ]

Now we can finally apply the max func­tion to this array which will give us the num­ber with the largest value, which since the array is in des­cend­ing order will be the first ele­ment, n-8. What we are left with is an algeb­ra­ic for­mula which we can sim­pli­fy one step at a time.

(n - 8 + n) / 2 % 4

(2n - 8) / 2 % 4

2(n - 4) / 2 % 4

n - 4 % 4

The mod­ulo oper­at­or % cal­cu­lates the remainder of an integer divi­sion, so any num­ber n % 4 will always res­ult in a num­ber between 0 and 3.

0 % 4 => 0
1 % 4 => 1
2 % 4 => 2
3 % 4 => 3
4 % 4 => 0
5 % 4 => 1
6 % 4 => 2
7 % 4 => 3

Since adding or sub­tract­ing 4 from n will not change the res­ult, we can sim­pli­fy the for­mula even further.

{{ n % 4 }}

Now all we need to do to cal­cu­late the dir­ec­tion in which to move, is plug a num­ber into n and we will get a value between 0 and 3, indic­at­ing in which dir­ec­tion to move accord­ing to the legend that accom­pan­ied the map. 

We could take it a step fur­ther and use the cycle func­tion to auto­mat­ic­ally give us a tex­tu­al rep­res­ent­a­tion of the dir­ec­tion to take for any giv­en n.

{{ cycle(['up', 'down', 'left', 'right'], n) }}

Finally, start­ing at house num­ber 25 and using the for­mula above res­ults in the fol­low­ing path.

{{ cycle(['up', 'down', 'left', 'right'], 25) }}   // down
{{ cycle(['up', 'down', 'left', 'right'], 37) }}   // down
{{ cycle(['up', 'down', 'left', 'right'], 19) }}   // right
{{ cycle(['up', 'down', 'left', 'right'], 31) }}   // right
{{ cycle(['up', 'down', 'left', 'right'], 33) }}   // down
{{ cycle(['up', 'down', 'left', 'right'], 69) }}   // down
{{ cycle(['up', 'down', 'left', 'right'], 51) }}   // right
{{ cycle(['up', 'down', 'left', 'right'], 35) }}   // right
{{ cycle(['up', 'down', 'left', 'right'], 40) }}   // up
{{ cycle(['up', 'down', 'left', 'right'], 28) }}   // up
{{ cycle(['up', 'down', 'left', 'right'], 24) }}   // up
{{ cycle(['up', 'down', 'left', 'right'], 11) }}   // right

But hey, why use a map scribbled on a scrap of paper when you can encode the map as a multi-dimen­sion­al array and write a recurs­ive macro to guide your sleigh? At least that’s what Patrick Har­ing­ton must have thought when he came up with his fant­ast­ic­al solu­tion, be sure to check it out.

{% set map = [
    [32, 16, 25, 37, 31, 64, 62],
    [47, 67, 37, 14, 77, 58, 11],
    [22, 35, 19, 31, 33, 16, 24],
    [34, 57, 95, 79, 69, 66, 28],
    [82, 65, 88, 14, 51, 35, 40],
    [72, 29, 18, 53, 47, 12, 22],
    [62, 74, 38, 63, 26, 73, 47]
] %}

A happy start to 2019 to everyone!!

Submitted Solutions

• Patrick Harrington

Solution submitted by Patrick Harrington on 27 December 2018.

{% macro guideMySleigh(map, y, x) %}
	{% import _self as macros %}
	{% if map[y][x] is defined %}
		{{ map[y][x] }} →
		{% switch map[y][x] % 4 %}
		{% case 0 %}
			{{ macros.guideMySleigh(map, y-1, x) }}
		{% case 1 %}
			{{ macros.guideMySleigh(map, y+1, x) }}
		{% case 2 %}
			{{ macros.guideMySleigh(map, y, x-1) }}
		{% case 3 %}
			{{ macros.guideMySleigh(map, y, x+1) }}
		{% endswitch %}
	{% else %}
		And to all a good night!
	{% endif %}
{% endmacro %}

{% set map = [
	[32, 16, 25, 37, 31, 64, 62],
	[47, 67, 37, 14, 77, 58, 11],
	[22, 35, 19, 31, 33, 16, 24],
	[34, 57, 95, 79, 69, 66, 28],
	[82, 65, 88, 14, 51, 35, 40],
	[72, 29, 18, 53, 47, 12, 22],
	[62, 74, 38, 63, 26, 73, 47]
] %}

{% set startingY = 0 %}
{% set startingX = 2 %}

{% import _self as macros %}
{{ macros.guideMySleigh(map, startingY, startingX) }}

• Philip Thygesen

Solution submitted by Philip Thygesen on 30 December 2018.

{{ n % 4 }} as the remainder will always be either 0, 1, 2 or 3